Why is max pump pressure used when sizing a hydraulic proportional DCV?

[Papajorgio]

When sizing a hydraulic proportional DCV all the charts specify pressure drop from P to T as being max pump pressure - load pressure. Out of curiosity why is max pump pressure used? And how would you best size a valve if load pressure is unknown?

I understand motion stalls once load pressure = max pump pressure, but in all other cases max pump pressure would be only load pressure + any pressure drops in the system, regardless of the pump compensator or pressure relief setting.

It has always bugged me to not know why. Thanks.

[Jacob_Paso]

Papajorgio,

To answer your question precisely, could you specify exactly which charts are you referring to? Some charts refer to P-A and B-T, some to A-B, and some to P-T.

I think perhaps there is some confusion as to the different situations. In a typical industrial hydraulic system used for high-performance motion control, the HPU supplies a constant pressure, regardless of the flow (up to a certain max flow, of course). The supply and demand of the system is sized such that constant pressure (within some tolerance) can always be maintained. The valves are closed-center valves. The HPU is either pressure-compensated, or a relief valve is used.

Typical mobile hydraulics are different. The pump is always pumping, and the valves are open-center. When the valves are open, supply pressure is very low. Pressure is built when the valves begin to close. This seems to be what you are referring to with the statement “in all other cases max pump pressure would be only load pressure + any pressure drops in the system”.

Our world of high-performance motion control deals only with a constant-pressure system. We are not interested in open-center systems, as they can’t provide as good control.

I suspect that when specs are given in terms of P-T, it simply means just that - the pressure drop between P and T. In a constant-pressure system, it won’t vary much. In open-center systems, it will.

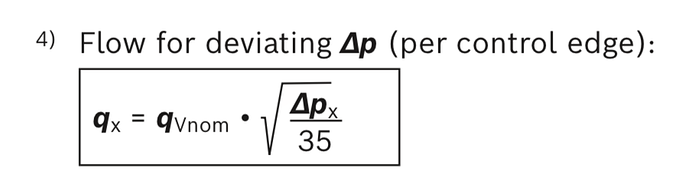
Perhaps some of the charts you refer to are performance limit charts, which I believe usually list P-T. Mainly, the performance limits are simply the formula of flow vs. pressure drop. This applies individually to the P-A and P-T, because, as you indicate, they can be different if a load exists. However, in valve datasheets, the performance specs are usually listed as tested with A directly connected to B. In this case, the pressure drops between A and B are equal if the spool is symmetrical, so the full P-T gives a good an idea of the performance limit.

Even in open-center systems, when we talk about the performance limit of a valve, the Bernoulli forces can overcome the spool, and flow may be reduced so that the limiting factor is not the normal flow vs. pressure drop formula. In this case, I believe the individual P-A and B-T flows and pressure drops are individually important, but my guess is that test cases imply equal flows and drops for simplicity of understanding and comparing between valves.

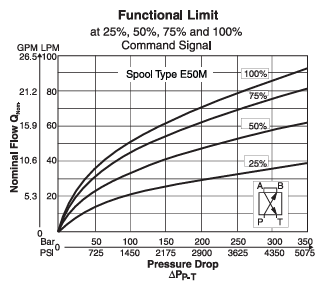
To illustrate, here is a performance chart of a Parker D1FP, which has a powerful linear motor that does not have significant impact by Bernoulli flow forces:

You can see the small hydraulic diagram shows that A and B are connected, so pressure drops are equal.

Here is a performance chart of a Parker D1FX, which has weak solenoids that do have significant impact by Bernoulli flow forces:

This chart does not show the hydraulic diagram of the test conditions, but I suspect that A and B are connected, so pressure drops are equal. You can see in this chart that after some point, as pressure increases, the flow decreases, which is problematic for motion controllers.

[ndzied1]

In my experience these valves are usually rated at a “nominal” pressure drop. 10bar, or 70bar and sometimes listed as 35bar per land depending on the valve and manufacturer.
These nominal ratings give you a way to compare and size valves. But the actual pressures are based on the load and change throughout the motion acceleration, constant velocity and deceleration phases of motion. And with single rod cylinders the pressure drop across each side of the valve is different.

For example the Rexroth 4WRPEH valve has a nominal rating at 70 bar total delta P. (35 bar per land). To calculate the flow at other pressures this equation is used.

I can’t imagine rating a valve at a maximum pump pressure since how would you know what pump is on a system.

[Papajorgio]

Thanks Jacob and ndzied1!

The Parker D1FP is a good example of what I’m referring to. The listed pressure drops are from P to T. If I understand this correctly, say the pressure comp is set to 200bar and flow is 35lpm, the valve is closed center, and moving the load requires 70bar. In the center condition system pressure will be 200bar, but when shifted 100% so flow is from P to A (or P to B), system pressure will be load pressure (70bar) + the valve pressure drop (approx. 50bar) = 120bar. I interpret this as min system pressure is 120bar and I can throttle flow till pressure drop = 130 bar because this will result in a system pressure of 200 bar which is my max setting due to the comp setting.

But in researching step by step methods for sizing a proportional valve, everything I’ve come across says pressure drop to be used on these curves = Pump pressure – load pressure. To me pump pressure would only be relevant when determining min command signal, but pump pressure – load pressure is used even at 100% open, see the attachments.

The rexroth attachment in particular has a pump pressure of 120bar and 150lpm, no load traverse pressure of 60 bar and selects a curve pressure drop of 60 because 120-60=60. Looking at the chart in the rexroth attachment, intuitively I think no load traverse pressure drop could be just 60bar (load pressure at traverse) +10bar (150lpm @ 100% intersects the 10bar line). So system pressure would be 70bar not 120bar.

Rexroth Hydraulic Trainer Vol 2 - Proportional Valve and Servo Technology.pdf (132.1 KB)

[ndzied1]

I think you are looking at the problem from the wrong direction. In the example, they setup the pump (fixed displacement) to be set at 120bar. So if the load takes 60 bar and, by problem definition, the pump is set at 120bar, the pressure drop from P to the loaded port of the valve will be 120-60=60bar.

But this thinking isn’t the whole story either. The valve meters in and out. So it takes pressure to move the oil that is leaving the actuator through the valve as well. I think they start the examples with equal area double rod cylinders so that all the flows are equal. In that case, it also takes 60bar to force the oil coming out of the cylinder through the valve. The pump has to supply this pressure as well. So it does take 120bar do this example.

Later on it that book I believe it goes over how to determine what system pressure you need for different applications.

Things get more complicated when you move to single rod cylinders where the flows on both sides of the valve are different. if you use a standard valve with a 1:1 spool with a single rod cylinder then you still have pressure drop from the pump to the actuator as

Delta P = Pump Pressure - Load Pressure

But coming back through the valve you have:

Delta P(side 2) = (Delta P(side 1)) / (Cylinder Area Ratio)^2)

The reason for spools with a 2:1 ratio are for use with cylinders that have area ratios around 2:1. So the flows across both sides of the valve can be close to equal.

[Papajorgio]

In the example with the pump set at 120bar, pressure to move the load being 60 bar, system pressure would achieve the pump setting of 120bar only when throttled 66%? At 100% system pressure would be 70 bar?

[ndzied1]

There is not enough information to say what the pressure would be based on the different valve setting. When things are moving, the pressures are ALWAYS dependent on the load. If this scenario is describing constant speed motion of a free mass then theoretically the friction will not change at a faster speed and the pressure would be the same… But if you wanted to get to the higher speed in the same amount of time the pressure of accelerating the load would be greater.

I believe this particular discussion in the book is intended to be a high level coverage of concepts and your brain is trying to dig deeper - which is a good thing.

For simple point to point moves, you generally have to look at at 6 phases of the motion to get the whole story. You should evaluate the pressure drops across both sides of the valve at these conditions:

1. Accelerating with cylinder extending
2. Constant speed with cylinder extending
3. Decelerating with cylinder extending
4. Accelerating with cylinder retracting
5. Constant speed with cylinder retracting
6. Decelerating with cylinder retracting

Not many people do all this and have developed rules of thumb that work or just oversize things to stay out of trouble. But sounds like you are wanting to understand deeper and this is part of it.

For certain scenarios you may calculate something that doesn’t make sense. At that point, you made a bad assumption or picked a pressure too low for the application.

[Jacob_Paso]

Papajorgio, I would like to clarify one thing: it is a mistake to think that system pressure will achieve some pressure. By definition, there is a pressure compensated pump in this system, which will provide a constant supply pressure. Therefore, you need to think about it the other way, as ndzied1 explained, starting out with a given system pressure, which is going to stay at that same pressure.

[Papajorgio]

Yes, I am trying to understand the reason behind the curves and calculations. It goes w/o saying that I trust the calcs and methods are correct, I mean they’re published and widely used.

Jacob this may sound like a dumb question but can you elaborate on “pressure compensated pump in this system, which will provide a constant supply pressure”? In application, the only way to set the comp is to dead head the pump, either by closing off the pressure port, throttling the DCV low enough, or applying enough load. If neither of the conditions exists system pressure will be < the comp setting so supply pressure is varying in that respect. Kind of like when ndzied1 said “When things are moving, the pressures are ALWAYS dependent on the load”. Intuitively I think one load being the degree to which the DCV is closed.

Me exploring the reasoning isn’t just an exercise. I’m responsible for design, testing, commissioning, and troubleshooting. I’ve just never had to size a proportional valve and am trying to understand it for an upcoming job. I know the calcs work but I just want to know why and I appreciate both you taking the time you have to help further my understanding.

Also, ndzied1 since you say “I can’t imagine rating a valve at a maximum pump pressure since how would you know what pump is on a system.” which follows my thinking. I know this is asking alot but how would you size a valve if the known system requirements are say a pressure comp pump flowing 60lpm, max system pressure can be 200 bar, pressure to move the load is 70 bar, and lets use the D1FP curve Jacob provided or another curve if the valve is not suitable for the hypothetical application. Accel and decel can be ignored, assume a valve and cylinder ratio to suit the curves used.

[Papajorgio]

Ok so I think I understand why Max Pump Pressure - Load pressure is used. It’s because throttling of flow will not occur until pressure drop = Max Pump Pressure - Load pressure. Let me know your thoughts.

[ndzied1]

My replies may be short and scattered, I have a lot going on right now but here’s the first step. You have to start with what you want/need the machine to do. At this stage don’t even think about the pump or valves.

What are the motions and forces that you need to create? If the machine does several things you have to find the worst cast scenarios throughout the machine cycle.

The velocities you come up with will lead to the flow rates required.

The forces you come up with will lead you to the pressures required.

There is interplay (engineering tradeoffs) here. Pick a larger cylinder and you need less pressure to make a force but more flow to make a velocity and vice versa.

I wouldn’t worry about a pump or valve until I had a handle on the above. There will be plenty of picking and repicking of valves and pumps when you get there.

[Papajorgio]

The realization that flow isn’t throttled until pressure drop = max system pressure - load pressure makes everything we’ve been talking about make sense.

Important notes being…

1. Why use a prop valve if it isn’t throttling flow? Using a prop flow dcv when pressure drop < max system pressure - load pressure, does nothing. Flow/load is not controlled under this condition.
2. For a pump to provide constant pressure, pressure drop must = max system pressure - load pressure.
3. Once max system pressure (comp setting) is achieved you cannot add more energy into the system. Therefore, flow must decrease.

[Jacob_Paso]

Papajorgio,

Let’s consider a simple industrial hydraulic system, consisting of a pressure-compensated pump that feeds a proportional valve, with the proportional valve controlling a cylinder. The pump has been sized such that it is capable of producing more flow at its set pressure than the max flow of the prop valve at that set pressure.

When the HPU starts up, the proportional valve is closed. The pump builds pressure in the system. Once pressure built, then we start controlling the prop valve. No matter how much the valve opens, the system pressure will always stay at the same set pressure (because the pump was sized to be able to supply enough flow at that pressure).

Your realization and important notes above are, in some respects (but not all), correct about when the pump is building pressure. However, it is still a bit of backward logic, because in any control situation, we are always starting with a constant system pressure, we don’t need to consider trying to build up to that pressure. And, the realization is kind of a moot point, because when we open the prop valve, we expect that the HPU has already before that reached system pressure and will continue providing a constant system pressure, and can do so at all the flow rates required by the system.

So, if we can accept and understand this, that system pressure is constant, then we can march forward and start understanding some of the things ndzied1 is talking about, which will help understand in detail how to size a system.

So here is some more understanding:
In the system above (with constant system pressure), consider what happens when we start opening the valve a bit. P flows into A, resulting in a building of pressure on the A side of the piston. This builds a force on the piston, which accelerates the rod and attached mass. Because the piston is moving, oil is forced out of B into T. The rod acceleration eventually ends and the cylinder continues moving at constant velocity.

There are several forces and pressure drops involved here. It is imperative to consider the forces needed to accelerate the mass. It is quite simplistic to assume a constant ‘load pressure’, as this assumes no acceleration, which is incorrect. This is why ndzied1 encourages considering acceleration, constant velocity, and deceleration, and the forces and pressure required.

-Jacob

[Papajorgio]

Thanks Guys,

It makes sense now. Jacob, your statement “No matter how much the valve opens, the system pressure will always stay at the same set pressure (because the pump was sized to be able to supply enough flow at that pressure)”. Is a good summary of why the books say pump pressure - load pressure = valve pressure drop. Abiding by this formula ensures the valve is sized so the system provides constant pressure. Not following this rule can result in an oversized valve, resulting in a loss of system pressure and flow control functionality at the higher command signals. Undersizing the valve results in the inability to achieve full system flow.

[Jacob_Paso]

Papajorgio,

One thing I want to make clear is that load pressure is not constant. In order to size the valve properly, it is important to make sure that the valve will provide enough flow at each point of the motion so that, after the P-A and B-T pressure drops over the valve, there is enough pressure differential on the piston to produce enough force to achieve the desired motion. This requires starting with considering the desired motions and forces, like ndzied1 states, then continue as he describes.

Notice that this analysis requires looking at forces and velocity, not just pressures. While the statement pump pressure - load pressure = valve pressure drop is correct, it is a very simplified statement, to the point that it can be misleading.

-Jacob

[Papajorgio]

I understand that. The whole reason for this post was to understand why pump pressure is used when sizing the valve.